Neredeyse bütün öğrencilerin merak ettiği, sınavlarda da sıklıkla karşılarına çıkan özel üçgenler ve bilinmeyen özel üçgenler geometrinin en temel konuları arasında yer alır.
Bu yüzden öğrencilerin geometri sınavlarına çalışırken özel üçgenler konusuna yeterince doğru çalışması gerekir. Sizlere içeriğimizde özel üçgenlere dair formül ve bilgilerden bahsedeceğiz.
Bir üçgen düzlemde birbirine doğrusal olmayan 3 noktayı birleştiren 3 doğru parçasının birleşimine özel üçgenler denir.
Özel üçgenler, özel koşulları olan üçgenlerdir. Bu koşullar, üçgenin kenar uzunlukları ve açılarının belli değerleri almasıdır. Özel üçgenler, genellikle matematik ve geometri derslerinde öğretilir ve bu üçgenlerin özel özellikleri sayesinde, çeşitli matematik problemlerinin çözümünde kullanılır.
Özel üçgenlerin diğer özel özellikleri de vardır. Örneğin, 30-60-90 üçgeninde, açılarının her biri 60, 60 ve 90 derece olduğundan, bu üçgenlerin açıları daima eşittir. Ayrıca, bu üçgenlerde, köşe noktaları arasındaki ilişki daima aynıdır ve bu nedenle, bu üçgenlerin simetrisi daima aynıdır. 45-45-90 üçgenlerinde de benzer şekilde, açıları daima eşittir ve simetrisi daima aynıdır.
Özel üçgenlerin diğer özel özellikleri, özel üçgenlerin çeşidine göre değişebilir. Örneğin, 7-24-25 üçgenleri, diğer özel üçgenlerden farklı olarak, kenar uzunluklarının asal sayılar olması nedeniyle özel özellikleri vardır. Bu özellikler, diğer özel üçgenlerden farklı olarak, bu üçgenlerin kenar uzunluklarının asal sayılar olması nedeniyle ortaya çıkar.
Özel üçgenlerin diğer özel durumları, özel üçgenlerin çeşidine göre değişebilir. Örneğin, 60-60-60 üçgenleri, diğer özel üçgenlerden farklı olarak, açılarının tamamının 60 derece olması nedeniyle özel özellikleri vardır. Bu özellikler, diğer özel üçgenlerden farklı olarak, bu üçgenlerin açılarının tamamının 60 derece olması nedeniyle ortaya çıkar.
Özel üçgenler, matematik ve geometri derslerinde çok sık kullanılan üçgenlerdir ve bu üçgenlerin özel özellikleri sayesinde, çeşitli matematik problemlerinin çözümünde kullanılır. Özel üçgenlerin özelliklerini iyi öğrenmek, matematik derslerinde başarılı olmak için önemlidir.
Özel üçgenler; ikizkenar üçgen, dik üçgen ve eşkenar üçgen olarak 3 farklı konuda ele alınır. Özel üçgen sınavlarına hazırlanan öğrenciler, düzenli test çözerek bilgilerini güncelleyebilir. Bu sayede geometri sorularının çözülmesi kolaylaşacaktır.
Açılarına Göre Özel Üçgenler
Açılarına göre üçgenler;
- 30 - 60 - 90 Üçgeni
- 30 - 30 - 120 Üçgeni
- 45 - 45 - 90 Üçgeni
- 15 - 75 - 90 Üçgeni
olmak üzere 4 tanedir. Bu üçgenler, geometrinin bütün konularında soru içerisinde mutlaka gelmektedir. Bu üçgenlerin özellikleri için okumaya devam edin.
30-60-90 Üçgeni
30-60-90 üçgeninde Hipotenüs, 90° nin karşısındaki sayıdır. Hipotenüsü gören açı en büyük açı olduğu için onu gören kenarda en büyük kenardır. 30-60-90 üçgeni geometri konusunda en çok karşınıza çıkan ve her üçgende kullanabileceğiniz bir kombinasyondur.
30-30-120 Üçgeni
Bu özel üçgende, 30° nin karşısındaki kenarların √3 katı hipotenüstür.
45-45-90 Üçgeni
Bu özel üçgende hipotenüs, 45° yi gören kenarların √2 katıdır. 45-45-90 üçgeni açı bulma konusundan en kolay üçgen açıları örneğidir. 45-45-90 üçgeni ikikenar üçgene de örnek olarak verebiliriz.
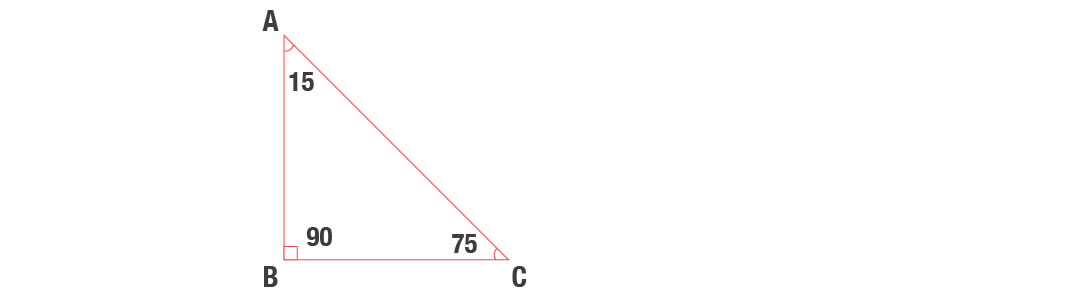
15-75-90 Üçgeni
Bu 15-75-90 özel üçgende yüksekliğin 4 katı bize hipotenüsü vermektedir. Yani, hipotenüse inen yükseklik ile 4'ü çarptığımızda ortaya çıkan sayı tekrar hipotenüs olarak bulunmaktadır. 15-75-90 üçgeni diğer açılarına göre üçgenlerden farklıdır. 15-75-90 üçgeni bir dar açılı üçgene örnek olarak verilebilir.
Özel Üçgenler: İkizkenar Üçgen Nedir?
Bir üçgende açıortay ve kenarortayı iki eşit parçaya bölen bir diklik iner. Bu diklik, üçgenin yüksekliğidir. Yükseklik, açıortay ve kenarortay olduğu için biri olduğu zaman diğerinin de olduğunu unutmayın. İkizkenar üçgende, her eşit kenarın elemanları birbirinin aynısıdır.
İkizkenar üçgende tabandan diğer iki eşit kenara paraleller çizilir. Daha sonra çizilen bu paralelleri toplarız. Sonuç, diğer kenarlardan birinin uzunluğuna eşittir.
Özel Üçgenler: Eşkenar Üçgen Nedir?
Bütün kenar uzunlukları birbirine eşit olan üçgene eşkenar üçgen denir. Üçgenin herhangi bir köşesinden indirilen yükseklik kenarortay ve açıortay oluşturur.
Kenarlarına Göre Özel Üçgenler
Kenarlarına göre üçgenler;
- 3 - 4 - 5 Üçgeni
- 8 - 15 - 17 Üçgeni
- 5 - 12 - 13 Üçgeni
- 7 - 24 - 25 Üçgeni
olmak üzere 4 tanedir. Bu üçgenler, geometrinin bütün konularında soru içerisinde mutlaka gelmektedir. Bu üçgenlerin özellikleri için okumaya devam edin
3-4-5 Üçgeni
Dik üçgenler arasında olan 3-4-5 üçgeni, kenar uzunluklarının 3-4-5 veya katları şeklinde olan üçgenlerdir. 6-8-10 üçgeni ve 9-12-15 üçgeni de tüm uzunluklar birbirlerinin katları olarak ilerlediğinden özel üçgen olarak kabul edilir. 3-4-5 üçgeni açıları ise 36,87 derece, 53,13 derece ve 90 derecedir.
8-15-17 Üçgeni
8-15-17 üçgeni, kenar uzunlukları 8-15-17 veya katları şeklinde olan üçgenlerdir.
5-12-13 Üçgeni
En çok bilinen özel üçgenlerden biri olan 5-12-13 üçgeni, kendi sayıları veya bu sayıların katları şeklinde yer alır.
7-24-25 Üçgeni
Her bir kenarı 7-24-25 veya bu sayıların katları şeklindeki üçgenlerdir.
Artık üçgenler konusunun geometrinin temel konularından olduğunu biliyoruz. ÖSYM sınavlarında önemli bir yere sahip olan bu konu için de detaylı bir çalışma göstermek önemli. Bu yüzden yapmanız gereken ilk şey, üçgen konuları için iyi bir çalışma göstermek.
Zorlandığınız veya çözemediğiniz sorular için destek almayı unutmayın. Öğretmen Tercihim' in uzman eğitmenleri ile geometri özel ders alın.





















Yazı Yorumları